October – 2010 – College Astronomy

A question was posed in Physics as follows:

An airplane is flying in a horizontal circle at a speed of 480 km/hr. If its wings are titled at a 40° angle relative to the horizontal, what is the radius of the circle (in km) in which the plane is flying? Assume that the required force is proved by the lift which acts perpendicular to the wing surface.

Now let’s identify the information that you need to know:

Velocity = 480 km/hr (133.3 m/s) (you need to convert this for the calculations to work right)
Angle = 40 degrees
Gravitational Acceleration = 9.8 m/s^2

What is important to note in this problem is that the force is modified by the 40 degree angle meaning that the circle can be tighter because the force is higher. The easiest way to do this is to use a derived formula. I’m going to shorten it a bit for time sake but you should be aware that it comes from this combination of horizontal and vertical forces:

$Horizontal - F_n\sin{\theta} = m\frac{v^2}{r}$
$Vertical - F_n\cos{\theta} - mg = 0$

This relationship gives us the following formula:

$\tan{theta} = \frac{v^2}{rg} \equiv r = \frac{v^2}{g \tan{theta}}$

Now we apply this to the known values to get our turning radius:

$r = \frac{133.3 m/s}{9.8 m/s^2 \tan{40}} \equiv r = 2160.83 m \equiv r = 2.16 km$

As always, please feel free to comment and or correct any conceptual or mathematical errors on my part. Thanks!

A question was posed in Physics as follows:

A 60 kg ball is tied to the end of a 50 cm long mass-less string and swung in a vertical circle. The center of the circle is 150 cm above the floor. The ball is swung at the minimum speed necessary to make it over the top without the string going slack. If the string is released at the instant the ball is at the top of the loop, how far to the right (in meters) does the ball hit the ground?

Okay, now we need to look up the key items in this question:

mass = 60 kg
radius = .5 m (50 cm)
height = 1.5 m (150 cm)
gravitational acceleration = 9.8 m/s^2
vertical circle (tossed overhead with release at the peak)
minimum speed for no slack ( t must be greater than or equal to 0)

Now, what this tells us is that we need to a) find the tangential velocity at the top of the circle, b) find the minimum tension on the rope that it won’t go slack at the top, c) the time that it takes the ball to fall back to the ground from it’s highest point (this will allow us to calculate distance on the x-axis). It is important to note that for this equation mass is extra information.

Let’s solve for the time from the top of the circle to the ground since that’s the easiest to get right away (a quick note, the peak is the height to the middle plus the radius of the circle, so, 2 meters):

$T = \sqrt{\frac{2d}{a}} \equiv T = \sqrt{\frac{2(2 m)}{9.8 m/s^2}} \equiv T = 0.64 s$

Conceptually we need to realize that the velocity of the object at the top of the circle will be related to the gravity, radius and tension. Since we want the minimum speed possible, that means the tension must be 0 or greater but not less than 0. That means that the tension goes out of the problem because we’re just dealing with gravity and the radius of the circle since tension is 0. That means we can figure out velocity based on the relationship between gravity and the radius of the circle:

$v = \sqrt{rg} \equiv v = \sqrt{2 m*9.8 m/s^2} \equiv v = 2.21 m/s$

Now that we have the velocity and the time that it takes for the object to get to the ground we use the very simple formula d = vt in order to find the distance the object travels on the x-axis.

$d = vt \equiv d = (2.21 m/s)(0.64 s) \equiv d = 1.41 m$

Ta-da! Hopefully this is somewhat helpful in explaining how to get this answer. Please feel free to comment and or correct me if you find errors.

*This post re-published & paraphrased from cache – September 30th 2009*

Since this is something that I recently had to do for a game that I’m a developer on, I thought it would be prudent to put together a write-up on the process of determining orbital period of a body around a central mass; specifically sidereal period. Overall, this is a fairly simple and straight forward problem, but, even so, it is certainly one that every Physics and Astronomy major and enthusiast should be familiar with.

Now, it should be noted that if an object of significant mass is orbiting a central mass, it is probably a good idea to include both masses in the calculation since it could change the result somewhat significantly. In order to perform this calculation we need to know the following:

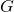$G$ , the gravitational constant
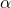$\alpha$ , semi-major axis (orbital radius or distance from object 1’s center to object 2’s center)
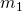$m_1$ , the mass of the central object
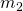$m_2$ , the mass of the orbiting object

So, with this information we can derive a formula from Kepler’s Third Law of motion; the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of it’s orbit.

$\frac{\alpha^3}{P^3}$

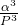
and Newton’s Law of Universal Gravitation; attractions are inversely proportional to the squares of the distances between massive bodies.

$F=G\frac{(m_1)(m_2)}{r^2}$

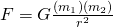
Now, the formulas need to be combined to achieve the following relationship:

$\frac{r^3}{P^2} = \frac{Gm}{4pi^2}$

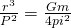
The resultant formula can now be manipulated into solving for 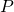$P$ or the period of the orbit as follows:

$\frac{1}{P^2} = \frac{Gm}{r^34pi^2} \equiv \frac{r^34pi^2}{Gm} = P^2 \equiv pi\sqrt{\frac{r^3}{Gm}} = P$

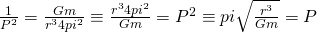
Important Note: Since we are using the total mass of the combined bodies we do not multiply the masses for this equation, if calculating the period for 2 large bodies the masses should be added together.

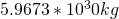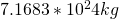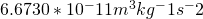Now that we have our formula, it’s time to work through our information. The central star is a Type A IV star at ~10,000K with a mass of $5.9673*10^30kg$ . The planet has a mass of $7.1683*10^24kg$ and an orbital radius of $5.2360*10^8km$ . Next we take this information, along with the Gravitational Constant ( $6.6730*10^-11m^3kg^-1s^-2$ and work through our formula:

$2pi\sqrt{\frac{(5.2360*10^8km)^3}{(6.6730*10^-11m^3kg^-1s^-2)((5.9673*10^30kg)+(7.1683*10^24kg))}} = P$

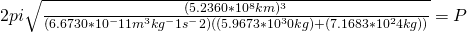
Now combine values and convert the orbital radius into meters so our units match:

$2pi\sqrt{\frac{(5.2360*10^11m)^3}{3.9820*10^20m^3s^-2}} = P$

$2pi\sqrt{\frac{1.4355*10^35m^3}{3.9820*10^20m^3s^-2}} = P$

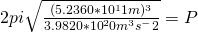
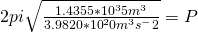
Now solve the rest:

$2pi\sqrt{3.6060*10^14s^-2} = P \equiv 2pi(1.899*10^7s) = P \equiv 1.1930*10^8s = P$

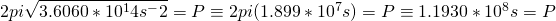
Great! Now we have our answer in seconds which means we can convert this number into years to obtain the yearly orbital comparison (the typical way to express orbital periods when it comes to astronomy). To do this we take our value, divide by 60 for the 60 seconds in a minute, by 60 again for minutes in an hour, by 24 for the hours in a day and then 365 for the days in a year.

[/math]1.1930*10^8s/60s/60m/24h/365d = 3.7830 years[/math]

And there you have it, our answer for the orbital period of the planet is 3.7830 times longer than that of Earths, or 3.7830 years.

In working through this I think there are a few common problems that can happen, so if you attempt this calculation and do not arrive at an answer you would expect, make sure to check the following things:

Make sure orbital period gets converted into meters at some point. The Gravitational Constant is calculated in meters which means your orbital radius value should be as well.
Make sure to add the masses of the bodies. This is important to note because other similar formulas (such as in calculating weight on another planet) masses are multiplied. This calculation uses total combined mass.
Check your units. If your calculations are complete but you did not net up with seconds for a unit your calculations could be flawed.

In closing, please let me know if you find any flaws with this write-up. I have put it together carefully, however, I am not immune to mistakes and have corrected several so far.

As you can see the site has undergone a lot of significant work and changes. Most of this is in attempt to make the site both easier to use while promoting community involvement. I was torn between the best ways to go about forum-like systems so I though that I’d give the current setup a try for now even though it is a little different.

I’ve installed buddypress which makes the site operate much more similarly to Facebook. The site has been re-themed and several other back-end modifications have taken place. Please register on the site and feel free to ask questions, post answers or use the chat rooms available to discuss things in real-time.

If you find something out of place, please let me know so I can resolve it as quickly as possible. Thanks!

Month: October 2010

Radius of a circle in relation to banking angle

Caclulating distance related to tangential velocity

Orbital Period Calculations

Site Update – October 2010

Copyright & Image Usage

Site Icon

Universe Today RSS

NASA Watch RSS