*This post re-published from cache – August 28th 2009*
In working on answering a question today, I was rather perturbed by the fact that I was not able to find a definitive answer to a question that I felt should be well defined. That question was: If I weigh 100lbs on Earth, how much would I weigh on Saturn?
Simple question right? Not by what I found online. There are a number of different sites that can be used to get a quick ( and possibly incorrect) answer. I found the sites that I visited in search of an answer to be at the least, inaccurate and at the most, dead wrong. The answers ranged from around 55lbs to about 115lbs. On top of this, the method for calculating weight on another planet was based on the gravitational acceleration at the surface. This is something that is defined already depending on the site or information you look at, but again, the values varied significantly.
Here’s an easy way to do it and get a reliable answer:
Find the gravitational acceleration, or more specifically the ratio of acceleration in relation to Earth, where Earth is a value of 1. Now, find a table online with the planet’s ratio that you want to calculate. For Saturn I used 1.065 (1.07 significant digits) found here. Simply cross-multiply to get your answer:
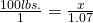
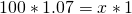
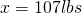
Now that we have the easy answer I think it is important to understand that without already having the gravitational ratio this is still calculable by obtaining the gravitational ratio on our own, as shown below.
Before we begin, it should be noted that the radius of a planet type body varies from point-to-point. This means that your answer will also vary depending on where you measure from. This could account for some of the discrepancies that I found on other sites. For example, you will be heavier at either of the poles and lighter at the equator. This is due to the bulge at the equator caused by rotation. This increases distance from the center of mass and reduces the gravitational forces on you slightly, causing you to weigh less. For our purposes, we will use the mean radius vs. a specific measurement.
First, we need my mass in kilograms (kg), rather than weight in pounds (lbs) so we use the formula here: 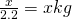
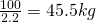
Great, now that we have the mass, we can move forward. We will need additional information at this point. The formula that will allow us to make further calculations, Newton’s Law of Universal Gravitation.
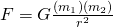
It should be noted that the value for  should be in meters, the values of
should be in meters, the values of 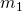 and
and 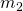 in kilograms and the resultant value of
in kilograms and the resultant value of 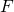 will be in Newtons.
will be in Newtons.
This formula will allow us to calculate the force exerted between objects of a given mass, at a given distance from the center of gravity. In turn, allowing us to calculate the respective weight. For this formula to work, we will need additional statistics. Since we are calculating for Saturn specifically, I took the values found from the NASA stats page linked earlier.
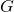 = The Gravitational Constant (
= The Gravitational Constant (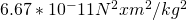 )
)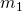 = Object 1 Mass, Saturn (
= Object 1 Mass, Saturn (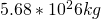 )
)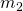 = Object 2 Mass, Person (
= Object 2 Mass, Person (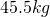 )
) = Mean Radius, Saturn (
= Mean Radius, Saturn (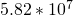 )
)
Now that we have all the variables needed, we can use Newton’s formula to get the result:
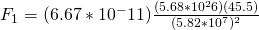
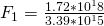
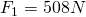
Now we have the gravitational force (F) for Saturn. In order to make a comparison based on weight, we will also need to do the same calculations for Earth. Since we already have the gravitational constant and our calculated mass, we need to acquire Earth’s mean radius and it’s mass in kilograms. These can both be found through the site linked earlier.
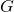 = The Gravitational Constant (
= The Gravitational Constant (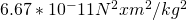 )
)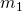 = Object 1 Mass, Earth (
= Object 1 Mass, Earth (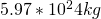 )
)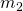 = Object 2 Mass, Person (
= Object 2 Mass, Person (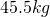 )
) = Mean Radius, Earth (
= Mean Radius, Earth (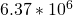 )
)
Once again we can use Newton’s formula to calculate the value of F:
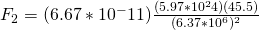
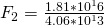
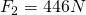
Now that we have both values we can compute the ratio:
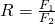 – where
– where 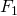 is the value of Saturn and
is the value of Saturn and 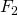 is Earth.
is Earth.
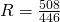
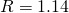
Curiously enough, the ratio arrived at in this equation is higher than the 1.065 cited in the NASA document. I am assuming this is due to differences in the value used for each planet’s radius. I will see what I can do about further investigating this discrepancy and amend my post if needed.
Now, to finish our process. We once again cross-multiply using 100lbs to 1 for the value on Earth.
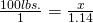
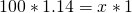
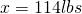
In conclusion, the variations in answer can be explained by taking into account the differences in radius values used in the calculations. Polar radius, Equatorial radius and mean radius will all give values slightly different from one another in a difference of 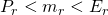 .
.
With our calculations it can be assumed that we have a possibility for error. Based on this information and given a discrepancy of a significant 7.4 lbs, this could account for roughly 7-13% variance in answers to this question. That said, make certain to note which radius measurement is being asked for when calculating these types of problems. It could mean the difference between a right and wrong answer.
![]()
![]()
![]()
![]()