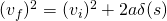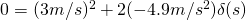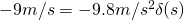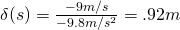Month: October 2010

Godspeed Shuttle Discovery & Crew!

tcrass 0 Comments

One final leap into the great blue yonder. May your ride be as free from bumps and thumps as much as possible (tall order to fill riding on top of some rockets) and may you safely depart and arrive after your mission is complete. I would love to be on the ground to see this one go up, but unfortunately it isn’t something that’s just not in the realm of possibility.

The crew has made it to Kennedy Space Center and if all goes well should launch into space for one final mission aboard the orbiter Discovery on November 1st around 4:40 PM EDT. Be sure to watch on NASATV

Discovery is the most flown orbiter in the fleet and among a massive repertoire of amazing accomplishments includes the launch of the Hubble Space Telescope and the missions to correct the optics and being the orbiter that returned us to space after the Challenger and Columbia disasters.

Space.com has posted a wonderful clip which summarizes Discovery’s career and historic accomplishments (in 3 parts). Give it a watch, the clips are only around 5 minutes each and very informative.

Shuttle Discovery Part 1

Shuttle Discovery Part 2

Shuttle Discovery Part 3

Two Blocks Colide and Move Up A Ramp

tcrass 1 Comment

Yet again a Physics problem for solving:

Two blocks are moving along a horizontal frictionless surface. The 4 kg block is moving to the right with a speed of 6 m/s and the 2 kg block is moving to the left with a speed of 3 m/s. The two blocks collide inelastically and then continue to move together along the surface and then up a 30° frictionless ramp. How high up the ramp does the combined object move?

Great!  To be honest this problem took me a little bit because I was making it quite a bit more complicated than was needed.  The easiest way to solve this is by breaking up the problem into 2 parts, solving the first with conservation of momentum and the second with simple linear kinematics.

So, let’s get down to business.  We have the following information that will be helpful to us.

Mass 1 = 4 kg
Velocity 1 = 6 m/s
Mass 2 =  2 kg
Combined Mass (they stick remember) = 6 kg
Velocity 2 = 3 m/s
Inclined Angle = 30 degrees
Gravitational Acceleration = 9.8 m/s^2

Now, we need to work out the first part.  We have to blocks moving in opposite directions that (by what the problem states) will stick together and continue moving at a certain velocity in a certain direction (by the problem we can assume toward the ramp).  So we use simple conservation of momentum as follows:

(P_fx)_1 + (P_fx)_2 = (P_ix)_1 + (P_ix)_2

(m_f )_1(v_f)_1 + (m_f )_2(v_f)_2 = (m_i )_1(v_i)_1 + (m_i )_2(v_i)_2

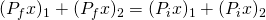
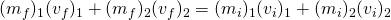
Since they stick together, our result will only be one result of m * v.  It is also important to note that because the second mass is moving toward the first, the sign for the second set will be negative, without this, you’ll definitely get the wrong answer.

(m_f)(v_f) = (4 kg)(6 m/s) + (2 kg)(3 m/s)

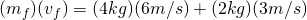
We also need to remember that we have our final mass already by adding the blocks masses since they stuck together, 6 kg.

(6 kg)(v_f) = (24 m/s kg) - (6 m/s kg) \equiv (6 kg)(v_f) = 18 m/s kg

(v_f) = \frac{18 m/s kg}{6 kg} \equiv v_f = 3 m/s

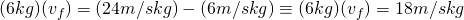
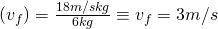
Wonderful!  Now we know how fast the blocks are moving after they combine and, consequently, when they hit the bottom of the ramp.  Now, we know that the incline of the ramp is 30 degrees from horizontal (x).  Because of this, we need to modify our acceleration due to gravity as a result.  This is important to find because it will tell us exactly how fast the blocks are slowing down.  If we know that, then we can use one of our simple kinematics equations to solve for the distance (as you’ll see).

Now, saving a lot of vector breakdown, the formula needed to find the modified value of gravitational acceleration is:

a = g\sin{\theta}

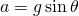
Now we simply plug in our values:

a = -9.8\sin{30} = -4.9 m/s^2

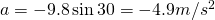
So, we know that the velocity the blocks reach the ramp at is 3 m/s and the acceleration due to the 30 decree incline is -4.9 m/s^2 and that to find the distance up the ramp they go, the final velocity will be 0 because at that point the blocks will start going back down the ramp.  Using the formula below we can plug in our calculations to find the final distance.

(v_f)^2 = (v_i)^2 + 2a\delta(s)

0 = (3 m/s)^2 + 2 (-4.9 m/s^2)\delta(s)

-9 m/s = -9.8 m/s^2\delta(s)

\delta(s) = \frac{-9 m/s}{-9.8 m/s^2} = .92 m

Rotational velocity and time related to artificial gravity

tcrass 0 Comments

Last on our Physics questions for today:

Future space stations and spacecraft may create “artificial gravity” by rotating. Consider a cylindrical space station with a radius of 894 m that rotates about its central axis. The inside surface of the cylinder is the floor of the space station upon which the astronauts live and work. What period of rotation (in s) is necessary for a 70 kg astronaut to have the same weight as he has on Earth?

Now let’s identify what we have:

Radius = 894 m
Astronaut Mass = 70 kg
Gravitational Acceleration (what we want it to be anyhow) = 9.8 m/s^2

The important thing to note is that we need to find the Normal Force being exerted on the astronaut as a result of the angular acceleration.  That force should be the equivalent of the Normal Force on Earth.  That pretty much tells us everything we need to get started.  Now, by this, we can figure the force intended by simple F = ma which gives us 686 N of force.  This is the Normal Force we want to attain.

Now, we need to find out at what velocity the cylinder needs to be spinning in order to obtain 686 N of force.  We can do this by using our angular velocity formula:

v = \sqrt{\frac{rF_n}{m}} = \sqrt{\frac{(894 m)(686 N)}{70 kg}} = 93.6 m/s

Easy as pie right?  Now that we have the velocity, we need to find the total circumference, this will give us the distance that the cylinder has to rotate through in order to complete 1 revolution.

c = 2\pi(r) = 2\pi(894) = 56.17.2 m

Now that we have the total distance and we have velocity, our handy-dandy formula for distance, velocity and time can be used.

d = vt \equiv t = \frac{d}{v} = \frac{5617.2 m}{93.6 m/s} = 60 s

And there you have it, it would take the space station 60 seconds to make one complete revolution in order to provide the same force on the astronaut as if on Earth.

As always, feel free to correct anything you see wrong with this.

Tension force related to angular velocity

tcrass 0 Comments

A question was posed in Physics class:

A toy “rocket-car” is attached to a metal rod that keeps the rocket moving in a horizontal circle on a frictionless table. The radius of the circle is 1.33 m, the mass of the rocket is 0.87 kg, and the rocket engine provides a thrust of 5.7 N. If the rocket starts from rest, how many revolutions will the rocket make before the tension in the rod equals 215 N?

Let’s pick out the important information from the equation:

Attached to a rod moving in a circle.
Radius (of the circle) = 1.33 m
Mass (of the rocket) = 0.87 kg
Thrust (of the engine) = 5.7 N
Final Tension Force = 215 N

Since it is going around in a circle on the table that is frictionless we can ignore gravity for this since it’s only 1 plane of motion.  The important thing to realize is that we need to find the relationship between tension on the arm and thrust of the engine which produces acceleration.  We know that as the object accelerates the tension increases.  We also know that if we can find the total distance traveled and divide it by the distance in one revolution, we’ll get the number of revolutions.

First, we will need to find out exactly how much the object is accelerating.  To get acceleration, we can work backwards since we have the force of thrust as 5.7 N.

F = ma \equiv a = \frac{F}{m} \equiv a = \frac{5.7 N}{0.87 kg} = 6.55 m/s^2

Now, we need to figure out what the velocity of the object is when the tension force is 215 N.  To do this, we use the formula for angular force which can be changed to angular velocity:

F = \frac{mv^2}{r} \equiv rF = mv^2 \equiv v = \sqrt{\frac{rF}{m}}

This will give us our velocity.  We already know the variables needed, r is 1.33 m, F is the final tension force, 215 N and our mass is 0.87 kg.

v = \sqrt{\frac{(1.33 m)(215 N)}{0.87 kg}} = 18.13 m/s

Now we have the velocity.  Getting the circumference is the easy part:

c = 2\pi(r) \equiv 2\pi(1.33 m) = 8.36 m

Great!  Now we have two more steps.  The first is to use our handy formula that deals specifically with velocity, acceleration and distance values and obtain the total distance:

v_f^2 = v_i^2 + 2a\Delta(s) \equiv \Delta s = \frac{v_f^2}{v_i^2 + 2a} = \frac{(18.13 m/s^2)}{(0)^2 + 2(6.55 m/s^2)} = 25.09 m

We’re almost done.  Now that we have the total change in distance we can do simple division and we’ll get our answer:

revolutions = \frac{\Delta s}{c} = \frac{25.09 m}{8.36 m} = 3.00 revolutions

And there you have it.  So the total times the object goes around the track before reaching 215 N of force on the arm is 3.

As always, please correct me if you see any problems.  Thanks!

Minimum velocity related to coefficent of friction

tcrass 0 Comments

A question posed in Physics class (much help to Judy for the assistance on this one):

One of the rides found at carnivals is the rotating cylinder. The riders step inside the vertical cylinder and stand with their backs against the curved wall. The cylinder spins very rapidly, and at some angular velocity, the floor is pulled away. The thrill-seekers now hang like flies on the wall. If the radius of the cylinder is 2.1 m and the coefficient of static friction between the people and the wall is ms = 0.390, what is the maximum period of rotation (in s) of the cylinder for the floor to be removed safely?

Now, what’s important to note out of all this is that you’re looking to get the angular velocity that will counter the force of gravity enough that static friction is effective in holding the people against the wall.

We know:

Coefficient of static friction = 0.390
Radius = 2.1 meters
Gravitational Acceleration = 9.8 m/s^2

We also know that static friction must be greater than or equal to the force and that must be greater than or equal to 0 in order to remain in place.  Anything less than 0 and the object moves.  So, we need 2 equations for this, one for the force related to gravity and one related to the normal force related to friction:

F_s = \mu_s(n)

F_g = ma \equiv F_g = mg

Now, the key to this is realizing that the normal force is related, or rather, equal to, the amount of force needed to keep the person in place.  The formula for that is:

n = \frac{mv^2}{r}

These can be combined as follows:

\mu_s\frac{mv^2}{r} = mg \equiv \mu_s\frac{v^2}{r} = g \equiv v = \sqrt{\frac{gr}{\mu}}

Now you can plug in numbers for the variables and get an answer for velocity.

v = \sqrt{\frac{(9.8 m/s^2)(2.1 m)}{0.390}} = 7.26 m/s

Now the second key to this is remembering that the distance around a circle is its circumference, that is the value that you’ll need to put in to get your velocity value spitting out seconds around.

\frac{2\pi(r)}{v} \equiv \frac{2\pi(2.1 m)}{7.26 m/s} = 1.8 seconds

And there you have it.  The minimum velocity that the cylinder needs to be spinning is 7.26 m/s which will cause it to rotate once every 1.8 seconds keeping the riders firmly in place.

As always, please correct me if you find any errors.