Month: June 2011

Calculating Diameter by Angular Diameter

tcrass 0 Comments

Question:
My name is Eva and I was wondering if you would be willing or able to explain to me the
a x r = S equation? I am on one of my labs and the problems involve the distances of planets from Earth a (radians), r (10 to the 6th power), and S (10 to the 6th power). So far for Jupiter I’ve figured out that a = 4.693e-3 and r = 588.5, but I am confused how to find S. For Saturn the equation was already done and read: 9.740e-5 for a, 1195.5 for r, and 0.1164 for S. How was this answer found?

—

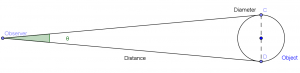
Okay.  So after a little investigation as to what exactly was meant by the question here, it relates to the calculation of diameter of an object in relation to the distance from the observer to the object and the angular size of the object at that distance.

Angular Diameter Representation

Angular Diameter Representation (click to enlarge)

a = angular size in radians
r = should actually be D for distance in kilometers
S = should be d for diameter of the object in kilometers

The labels make little difference if you understand how they are to be used.  I think that’s the biggest hurdle in this problem.  See diagram for graphical representation.

 

Now, the information that we have is as follows:

a = 9.740e-5 radians is roughly the angular size of Saturn viewed from Earth.
D = 1195.5e6 km is roughly the distance to Saturn.
d = what we’re searching for.

So, by our formula: a * D = d (or a x r = S if you like),

a * D = d; (9.740 * 10^-5 radians) * (1195.5 * 10^6 km) = 0.1164417 * 10^6 km

So the diameter of Saturn, based on our calculations using the angular size and distance to Saturn, is about 116,441 km.

Trigonometry Simplify – sin^4x – cos^4x

tcrass 4 Comments

I thought I’d post this quick simplification using trig identities since it gave me a bit of a run for my money.  Partially so I remember it better and second, to lend a bit of help to those who might be stuck.

The Problem: Simplify sin^4 x - cos^4 x

Now, how hard could this be?!?  As it turns out, it’s not too bad, but the trick is in factoring what we have.

Factor things out: (sin^2 x - cos^2 x)(sin^2 x + cos^2 x)

Great!  Now that we have this in better form we need to bring in a couple of trig identities which will help us solve this and one that I’m going to cite because it could trick you!

Pythagorean Identity 1: sin^2 x - cos^2 x = 1
Pythagorean Identity 2: 1 - cos^2 x = sin^2 x
Pythagorean Identity 3: sin^2 x + cos^2 x = cos(2x) (This is the tricky one!  As much as it seems like we could use this identity we would end up loosing terms.  Don’t use this)

Now, things should start looking a bit simpler to solve.  So, here we go starting with what we factored:

1) (sin^2 x - cos^2 x)(sin^2 x + cos^2 x)
2) Use Identity 1 to substitute for the first term: (1)(sin^2 x + cos^2 x)
3) Use Identity 2 to substitute for the first part of the second term: (1)(1 - cos^2 x + cos^2 x)
4) Now combine the two like terms: (1)(1 - 2cos^2 x)
5) And so we have it!  The final result is: 1 - 2cos^2 x

Now, looking back, if you notice in identity 3, if you use it, you end up with a term (1)(cos(2x)) which multiplied out you loose the negative and the 2 in front of cos.  This is a big problem because if you did it this way, what you get in the end does not equal what you had in the beginning and thus, isn’t a valid way to simplify this problem.  As a result, you must use identities 1 and 2 as shown in the 5 steps above.

Cheers!

65 Years – xkcd

tcrass 0 Comments

Completely worth sharing…

65 years after we first walk on the moon...

The universe is probably littered with the one-planet graves of cultures which made the sensible economic decision that there's no good reason to go into space--each discovered, studied, and remembered by the ones who made the irrational decision.