I’m writing this article because I felt that it was significant to understanding a good deal of physics and astronomy aspects that rely on this type of mathematics. By the very title, I’ve implied the need to apply the big bad demon known as Calculus. Had I better understood this part of calculus sooner it would have made a significant difference in my ability to handle some of the more complex physics problems. As a result, I thought I would share in hopes that this might help someone in the future.
Although this article will focus on the shortcut methods to working out some of the problems presented and the need for in-depth understanding of calculus is not needed. To make sense of everything the reader should have a handle on basic geometry and trigonometry as well as some familiarity with the following calculus topics:
- Functions
- Continuity and Limits
- Differentials
- Partial Differential Equations
So, let’s begin with the classic melting snowball problem:
A spherical snowball is melting in such a way that its radius is decreasing at rate of 0.5 cm/min. At what rate is the volume of the snowball decreasing when the radius is 3 cm. (Note the answer is a positive number).
Step 1: Identify what we have and what we’re looking for.
Radius: 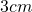
Decreasing Rate: 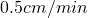 decreasing radius
decreasing radius
Additional Information: We also have a sphere and we know that the sphere is decreasing which means that it’s volume is also decreasing. Thus, we need the formula for the volume of a sphere since that’s what’s changing: 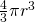
Step 2: Now for the trick. One very handy piece of calculus that allows us to handle related rates problems is differentiation, specifically the differential. It is important to note that this is not exactly the same thing as taking the derivative, but that action is one process in this problem. The resulting formula for this process is:
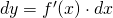
Step 3: To break this formula down a bit, dy (since we’re working with volume this will be dV for us) is the part you’re looking for in this problem; solving for it will give you the rate at which the volume is changing in relation to the radius of the sphere. The next part, f'(x) is the derivative of the formula that you’re working with, in this case, the formula for the area of a sphere. Finally, dx is the current value of the rate of change (or slope of the tangent line to the function at the given point, if that makes more sense) of whatever it is we happen to be looking for. In this case, it would be the rate that the radius of the sphere is changing.
Step 4: Now that we’ve established our variables and the equation needed to solve this problem we can set up the problem further.
We must find the derivative of the equation of the volume of a sphere:
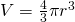
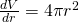
Now, substitute in the values into our differential:
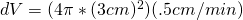
Now solve:
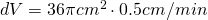
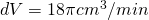 or
or 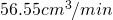
And there we have it; when the radius of the snowball is 3 centimeters, the volume of the snowball is decreasing by 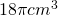 or
or 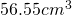 every minute! It must be one hot day out!
every minute! It must be one hot day out!
Stay tuned for a few follow up problems related to this article.
![]()
![]()
![]()
![]()
![]() (This is the tricky one! As much as it seems like we could use this identity we would end up loosing terms. Don’t use this)
(This is the tricky one! As much as it seems like we could use this identity we would end up loosing terms. Don’t use this)![]()
![]()
![]()
![]()
![]()
![]() which multiplied out you loose the negative and the 2 in front of cos. This is a big problem because if you did it this way, what you get in the end does not equal what you had in the beginning and thus, isn’t a valid way to simplify this problem. As a result, you must use identities 1 and 2 as shown in the 5 steps above.
which multiplied out you loose the negative and the 2 in front of cos. This is a big problem because if you did it this way, what you get in the end does not equal what you had in the beginning and thus, isn’t a valid way to simplify this problem. As a result, you must use identities 1 and 2 as shown in the 5 steps above.